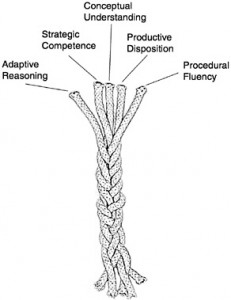
The Five Strands of Mathematics Proficiency
DEVELOPING MATHEMATICIANS
National Research Council. (2001). Adding it up: Helping children learn mathematics. J Kilpatrick, J. Swafford, and B. Findell (Eds.). Math Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
For more info http://books.nap.edu/catalog.php?record_id=10434
Click on each strand for classroom structures that promote this strand:
The Five Strands of Mathematics Proficiency
VISIBLE THINKING STRATEGIESCore Teaching Practices from the Principles to Action, NCTM (2014) Implement tasks that promote reasoning and problem solving. Effective teaching of mathematics engages students in solving and discussing tasks that promote mathematical reasoning and problem solving and allow multiple entry points and varied solution strategies. Support productive struggle in learning mathematics. Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships. Build procedural fluency from conceptual understanding. Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems. Establish mathematics goals to focus learning. Effective teaching of mathematics establishes clear goals for the mathematics that students are learning, situates goals within learning progressions, and uses the goals to guide instructional decisions.
Elicit and use evidence of student thinking. Effective teaching of mathematics uses evidence of student thinking to assess progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning http://books.nap.edu/catalog.php?record_id=9822 Jennifer Suh, Assistant Professor, Graduate School of Education, College of Education and Human Development teaches an EDCI 552 course, Mathematics Methods for the Elementary Classroom, at George Mason University’s Fairfax Campus. Photo by Alexis Glenn/George Mason University |
